This article includes universal curves of the effects of source temperature on the space-charge-limited extraction of charged particles to form beams. The main result is that the current density may exceed the Child limit (discussed in a previous article) when the thermal energy of source particles (kT) is a significant fraction of the extraction energy (qV0). By universal curves, I mean that the graphs apply to both electrons and ions at any source temperature and non-relativistic extraction voltage. The generality follows from the use of scaling relationships.
The space-charge-limited flow of electrons across a vacuum acceleration gap is a process of practical importance in the design of wide variety of electron-beam equipment. I previously discussed the theory of flow with a singular electron distribution. The zero-energy model raises some logical issues:
- If all electrons on the surface are identical, what determines whether an individual electron enters the flow?
- How can we account for a flux to the surface if the electrons are cold?
For a realistic model, we must include a thermal distribution of incident electrons. The initial electron energy has two effects on beam extraction:
- For low-voltage injectors, initial electron thermal energy increases the space-charge-limited current density.
- Transverse components of thermal energy limit the emittance of the extracted beam.
The theory with an energy-distribution is more difficult. Analytic treatments developed in the 1930s involved complex equations whose solution required limiting conditions. These difficulties may be circumventing with a numerically-exact computer calculation. A full discussion of the methods is given in the paper Cathode thermal effects in one-dimensional space-charge-limited electron flow. Here, I'll concentrate on scaling laws and the results.
The key is to identify a minimal set of control parameters. One fundamental quantity is the ratio of the available current flux from the thermionic source to the Child-law current density for a cold source, jt/jc. If jt = jc, then every particle is extracted and |Ez| is almost zero at the source surface. If we raise the source temperature so that jt > jc, a region of depressed potential is created as in Figure 1. The potential barrier Vm at position xm allows only a fraction ~jc/jt of the incident electrons to pass. Note that for given source density and temperature kT and extraction voltage V0, both fluxes scale as 1/√m.
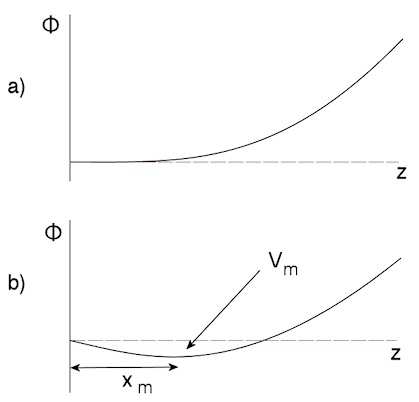
Figure 1. Variation of electrostatic potential near the surface of a cathode under the condition of space-charge-limited emission. a) Zero-temperature electrons. b) Hot electrons.
A second control parameter follows from the invariance of non-relativistic particle trajectories in an electrostatic field. Suppose we inject a particle with an initial kinetic energy U0 into a complex three-dimensional electrostatic field created by an electrode set with voltages Vi. The trace of the orbit in space is independent of particle mass, while the time to move along the trace is proportional to ?m. If we change the input energy and all voltages by a factor of β, then the trace is unchanged and the transit time scales as 1/√β. It is straightforward to verify these rules with a code like Trak. The implication is that the solutions are self-similar if we apply scaling of fluxes by jc (Child current density for zero source temperature) and scaling of source temperature by kT/qV0. If we perform one set of calculations for electrons at qV0 = 100 eV, then the scaled results may be applied to all particles at all extractor voltages.
I investigated a range of relative electron temperatures 0.001 ≤ kT/qV0 ≤ 0.100. For each value of (kT/qV0), the code carried out a series of runs over the range of thermal flux 1.0 ≤ jt/jc ≤ 5.0. The upper limit reflects the fact that it would be impractical to run a cathode at very high temperature to create a thermal current flux much higher than the extractable current density. Figure 2 shows raw data for (kT/qV0) = 0.05. At (jt/jc) = 1.0, all electrons were transmitted. Reflected electrons occurred when the thermal flux exceeded the temperature-adjusted space-charge limit. At high values of (jt/jc), the reflected current increased without limit while the transmitted current density approached a constant value. For lower values of (kT/qV0), saturation occurred at lower values of (jt/jc).
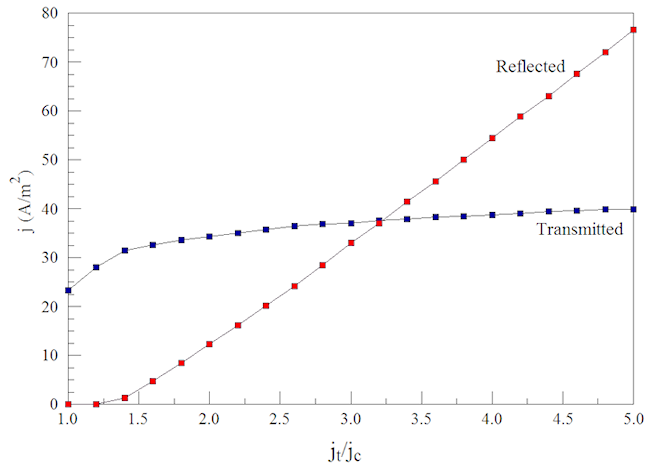
Figure 2. Transmitted and reflected current as a function of (jt/jc) for kT/qV_0 = 0.05.
Figure 3 is a normalized plot of saturated transmitted current density js for the full set of runs. Note that the values converged to 1.00 when (kT/qV0) ≪ 1.0, a good check of the numerical accuracy of the code. The dashed line is a fit to the data:
js/jc ≅ 1.0 + 3.68 (kT/qV0)^0.55.
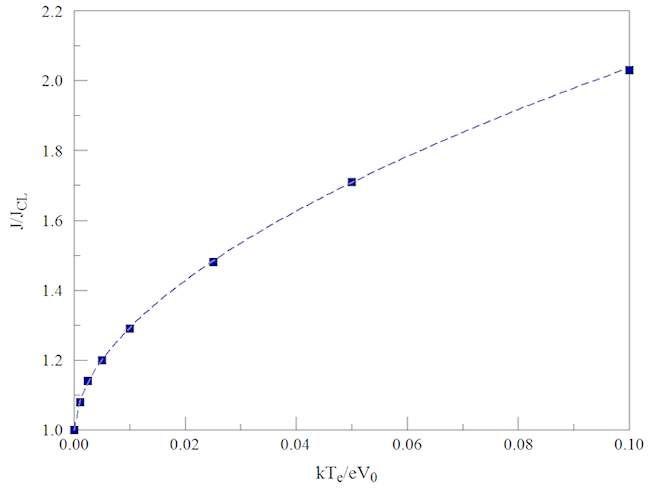
Figure 3. Normalized transmitted current density as a function of normalized temperature for (jt/jc) ≫ 1.0.
The code results can be used to create plots of the scaled sheath properties, Vm and xm (Figure 4). Note the use of scaling properties to compress all the data on to the plots. As expected, Vm and xm increased with (jt/jc).
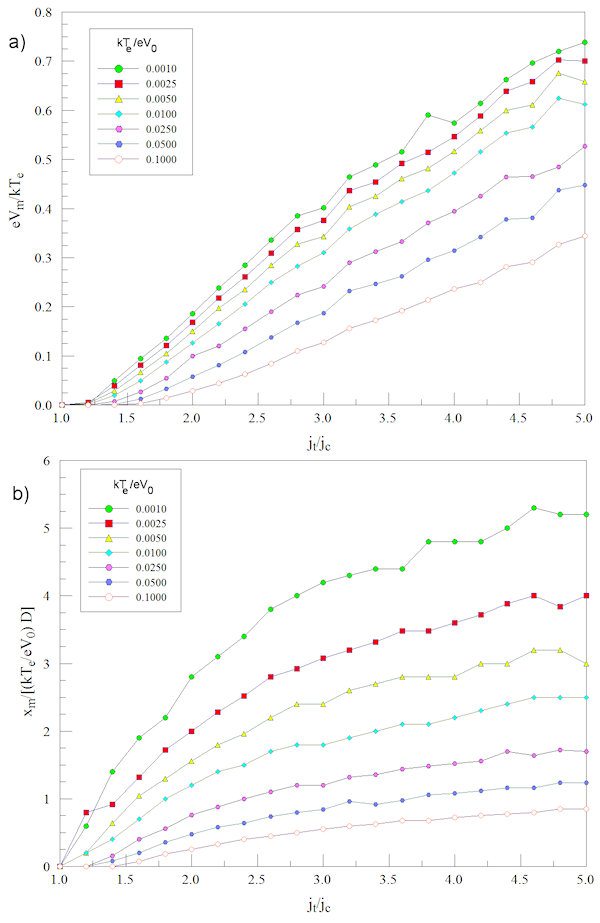
Figure 4. Calculated sheath properties. a) Normalized potential barrier height as a function of (jt/jc). b) Normalized sheath width as as a function of (jt/jc).
I also used the code to resolve a long-term question in my mind. Could sheath processes contribute to changes in the transverse temperature of the transmitted beam? My original thought was that velocity selection at the sheath could lead to beam cooling. At high values of (jt/jc), only electrons with the highest longitudinal energy could cross the potential barrier to contribute to the transmitted beam. Perhaps these electrons would, on average, have lower transverse energy. Under this theory, the angular divergence of the transmitted beam would decrease with increasing (jt/jc). Accordingly, I included routines in the code to collect only transmitted electrons in the converged solution and to analyze their root-mean-squared divergence angle. Figure 4 shows the results. The divergence increased with kT as expected, but there was no dependence on (jt/jc). In retrospect, this was precisely the behavior one would expect from theory. Because there are no forces in the x and y directions, the transverse temperature of the particles was invariant. In the presence of a potential barrier, the density of particles in a Maxwell-Boltzmann distribution changes, but the temperature does not. In other words, the velocity distribution f(vz) is the same at all positions z > xm. Therefore, the ratio of transverse to longitudinal spread does not depend on the height or position of the sheath. Note that the slight decrease in angle at the highest temperature is the result of truncating the Maxwell-Boltzmann distribution. This is a good example of the steadying effect of numerical calculations when intuition go awry.
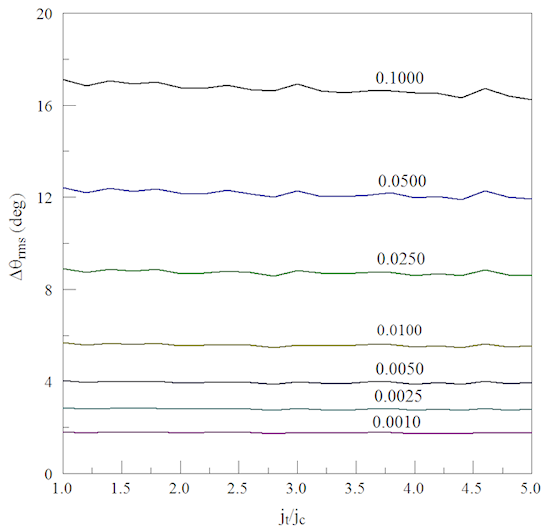
Figure 5. Root-mean-squared divergence angle of the transmitted beam as a function of (jt/jc) and (kT/qV0).
LINKS