To illustrate a Magnum calculation of the holding force of a permanent-magnet assembly, what better example than a refrigerator magnet (RM)? Certainly, the mass of RMs in use throughout the world exceeds that of the Large Hadron Collider.
Figure 1 shows the geometry of a high-quality RM. The magnet is a button of NdFeB with diameter 0.5", height 0.25" and remanence field Br = 1.26 tesla. It is magnetized in the vertical direction. The steel flux return has thickness 0.125", width 1.00" and depth 0.75". The refrigerator is represented by a steel sheet of thickness 0.0625". The magnet assembly is molded into a plastic case so there is a 0.0625" gap between the refrigerator and the lower surfaces of the magnet and flux return. There is also an adorable plastic bunny above the assembly. We shall assume that the rabbit has μr = 1 and exclude him from the model.
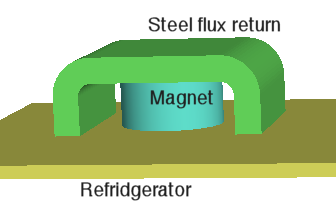
Figure 1. Refrigerator magnet example, geometry.
To start, we must make decisions in two areas:
- The size of the solution volume.
- The material model for the steel.
With all the steel, the magnetic flux will be localized to the assembly. Therefore, it's not necessary to include a lot of surrounding space. I picked a width of 2.00" in x and a depth of 1.50" in y for the solution volume. The volume extended from -0.25" to 0.50" in z with the lower surface of the magnet at z = 0.0. With good use of variable resolution, I was able to get an accurate calculation with only about 90,000 elements.
The choice of material model relates to a discussion in another article. Should we attempt to find permeability values for the steel and do a full nonlinear model with Magnum? Probably not, for the following reasons. First, if the steel pieces are driven to saturation, then the magnet is too big for the assembly. We would be paying for extra expensive magnet material that is not reflected in a higher holding force. Second, if the steel is not in saturation then it doesn't matter what value of μr we use as long as it is large compared to unity. The best strategy is to assume a resonable fixed value of μr for the steel and perform the calculation. If parts of the steel are driven above 2.0 tesla, then we need to rethink the geometry.
The Magnum calculation took about about 70 seconds. Figure 2 shows a plot of |B| over a plane normal to z in the refrigerator plate. The peak field is only 1.15 tesla. Further, we find that the field in the steel return is small, with only a small region that reaches |B| = 1.60 tesla. Therefore, the assumption of unsaturated iron is valid. I used the automatic Maxwell stress tensor calculation in Magview to find the force. Here is a script to control the calculation:
* NReg RegName
* =============================
* 1 AIR
* 2 MAGNET
* 3 STEELRETURN
* 4 STEELPLATE
OUTPUT REFRIGE
INPUT REFRIGE.GOU
* Magnet + Steel
FORCE 2 3
* Lower plate
FORCE 4
ENDFILE
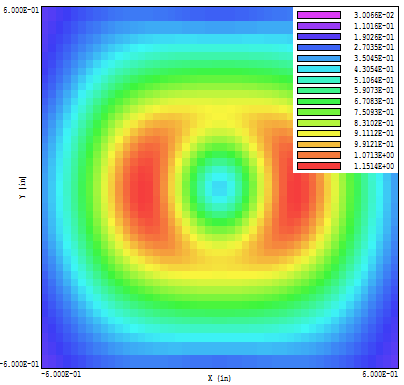
Figure 2. Refrigerator magnet example, field in the plate.
As expected, there was only an axial component. The results were Fz(magnet and steel) = -16.260 N and Fz(refrigerator) = 17.817 N. There is some difference. The integral over the flat lower plate should be quite accurate, but we expect reduced accuracy for the magnet-steel assembly because it has a complex shape with sharp edges. In a second calculation, I surrounded the assembly with a diagnostic region, a box with ?r = 1.0. The field values had a smoother variation on the box surface and the Maxwell integral has the same value over any surface that encloses the magnet and steel. The result for this calculation was Fz = -17.671 N, in good agreement with the integral over the lower plate. The pull force in pounds is 17.81*2.205/9.81 = 4.00 lbs, an impressive figure high enough to attach a real rabbit to the refrigerator.
Use the following links if you would like to run the example:
refrige.min
refrige.gin
refrige.scr
LINKS