The Maxwell stress tensor may be used to calculate electric and magnetic forces on objects. The method is seldom introduced in introductory texts on electromagnetism. Advanced texts often present the Maxwell stress tensor as a mathematical abstraction without explaining why is is useful. In reality, the method is critical for practical force calculations in numerical codes. In this article, I wanted to review some of the theory and emphasize the specific reasons why the method is used. To illustrate, I will concentrate on magnetostatic forces.
Most people are familiar with the Lorentz force density f = j × B from basic electromagnetism courses. The vector quantity f is the force per volume in a region with magnetic flux density B and current density j. The total magnetic force on an object is given by a volume integral of the force density over its volume (Eq. 1). It is important to recognize that the quantity j is the total current density within the object, the sum of applied and atomic contributions. The applied current density arises from currents in coils. The magnitude, location and direction of the applied current density follows from the known coil geometry and drive currents. Therefore, is relatively easy to apply Eq. 1 in numerical codes to find coil forces. In contrast, volume integrals are not practical to find force contributions from active materials im magnetic field calculations (field excluders, iron and permanent magnets) and dielectrics in electric field calculations. In these cases, the current or charge may be concentrated in thin surface layers.
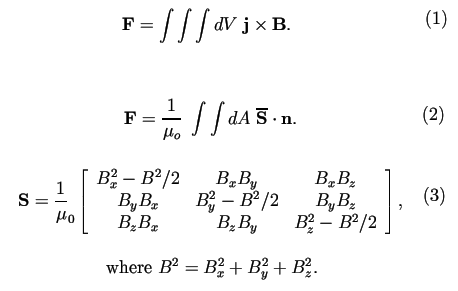
Equation 2 shows the total magnetic force on a body determined from the Maxwell stress tensor of Eq. 3 (for complete derivation for the electric and magnetic cases, see the tutorial at http://www.fieldp.com/documents/stresstensor.pdf). There are two important differences from Eq. 1:
- The expression involves a surface integral around the object rather than a volume integral through the object.
- The force is determined entirely from the magnetic flux density B outside the object.
As a result of these features, there are three reasons why Eq. 2 is is better suited to a numerical calculation than Eq. 1:
- The accuracy of the integral is not affected by the distribution of current density within the object. In particular, the thin surface layers of magnetically-active materials present no problem.
- The surface need not coincide with the physical surface of the object. If the object has sharp corners and regions of field enhancement, we can improve accuracy be using a diagnostic surface outside the physical surface.
- The integral depends only on the field distribution outside the object. It is not necessary to know the exact current density distributions within complex anisotropic or nonlinear materials.
Some care must be exercised in applying the method. Because the integral determines the force on all applied and material currents inside the surface, we must avoid ambiguities of the enclosed current. The surface must be in an air region surrounding the object. Here, the term air implies that the region contains no material currents (μ = μ0). The figure illustrates the logic of the calculation. If we have an assembly of ferromagnetic and permanent-magnet objects surrounded by an air volume, then we can take the integral of Eq. 2 over any enclosing surface. One choice is the outer boundary of the assembly components (designated surface A in the left-hand figure). In this case, we evaluate magnetic field values in the air elements near the surface to ensure that the integral encloses all material currents of the object. We could also define an arbitrary surface by enclosing the assembly inside a diagnostic air region. The integral over the surface marked B gives the same result (to within the numerical accuracy of field interpolations). The right-hand figure shows a case where the stress tensor integral may not give the correct result. In this case the integral extends over the surface of ferromagnetic region A that is in contract with another iron or permanent-magnet region (B). The field values in region B along the common boundary include contributions from surface currents of both regions. The calculation therefore gives the force on region A plus an indeterminate portion of the force on region B.
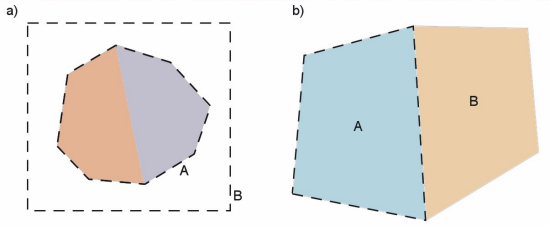
Valid (left) and invalid (right) applications of the stress tensor
Finally, you can also calculate torques arising from electric and magnetic forces by the surface integral method. The following tutorial reviews the forms of the Maxwell stress tensor for both electric and magnetic fields and gives a general expression for the electromagnetic torque tensor: http://www.fieldp.com/documents/forceandtorque.pdf.
LINKS