I recently consulted on issues of corona discharges from equipment near high-voltage power lines. It was an opportunity to review material from my book Principles of Charged Particle Acceleration. Corona is a practical topic of general interest, so I decided to include the information in this note. This article deals with a necessary preliminary: the physics of breakdowns in gas insulators. A following article will cover the specific application to corona discharges. For reference, you can request a download of the complete book in PDF format at http://www.fieldp.com/cpa.html.
Gas insulation is used is used extensively in high-voltage power transmission for two reasons:
- Gas can recover its insulating properties after a breakdown.
- It's free.
In this application, it is critical to ensure that voltages and electric fields are well below levels that can lead to a self-sustained breakdown. To derive the breakdown conditions, first consider the one-dimensional gas-filled gap of Figure 1. The electrodes have separation d and the applied voltage is V0. There is no charge flow between the electrodes at low voltage. We want to determine how a large interelectrode current can be initiated at high voltage.
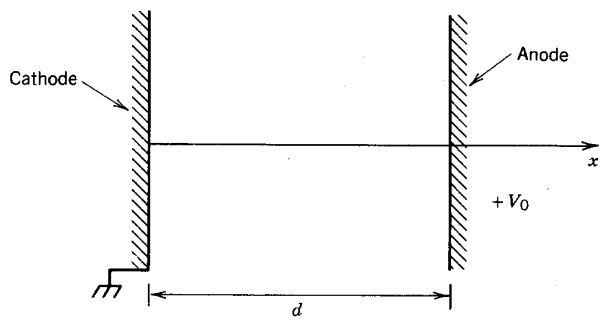
Figure 1. One-dimensional gas-filled gap.
Suppose that a few electrons are produced on the negative electrode (possibly caused by photo-emission from cosmic rays or ultraviolet light). The small source current density leaving the electrode is represented by j0. The electrons are accelerated by the applied field and move between the widely spaced gas molecules, as shown in Figure 2a. In a collision with a molecule, an electron is strongly deflected and much of its kinetic energy is absorbed. As a simplification, assume that electrons are accelerated between molecules and lose all their directed energy in a collision. The parameter λ is the mean free path, the average distance between collisions. The mean free path is inversely proportional to the density of gas molecules. In turn, the density is proportional to the pressure, p, so that λ ~ 1/p .
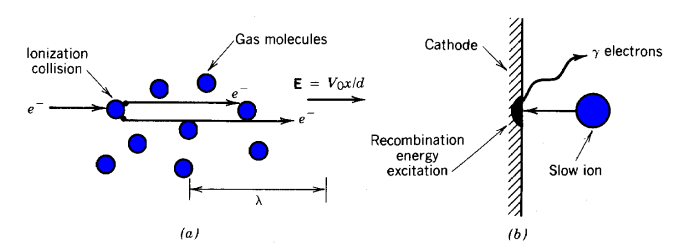
Figure 2. Processes in a gas-filled, high-voltage gap. a) Electron migration in the presence of an electric field. b) Liberation of electrons on the negative electrode by ion recombination.
The average energy gained by an electron between collisions is given by Eq. 9.33. An election may ionize a molecule in a collision if ΔT is high enough (ΔT > 30 eV). In the ionization process, the excess kinetic energy of the electron drives an electron out of the molecule, leaving a positive ion. The two electrons move forward under the influence of the field, producing further electrons. The current density increases geometrically along the electron drift direction. The ions drift in the opposite direction and do not contribute to ionization in the gas. The motion of drifting ions is dominated by collisions; generally, they cannot reach high enough velocity to eject electrons in a collision with a molecule.

Electron multiplication in a gas with an applied electric field is characterized by α, the first Townsend coefficient [J. S. Townsend, Electricity in Gases, Phil. Trans. A193, 129 (1900)]. This parameter is defined by Eq. 9.34. Consider an element of length Δx at the position x. The quantity n(x) is the density of electrons at x. According to the definition of α, the total number of additional electrons produced in a volume with cross-sectional area dA and length Δx is given by Eq. 9.34a. Dividing both sides of the equation by dAΔx, and taking the limit of small Δx leads to Eq. 9.35. The solution of the equation implies an exponential electron density variation. Expressed in terms of the current density of electrons (assuming that the average electron drift velocity is independent of x), Eq. 9.35 implies the result of Eq. 9.36 if the negative electrode is located at x = 0. The current density arriving at the positive electrode is given by Eq. 9.37.
Although the amplification factor may be high, Eq. 9.37 does not imply that there is an insulation breakdown. The current stops if the source term is removed. A breakdown occurs when current flow is self-sustaining, or independent of the assumed properties of the source. In the breakdown mode, the current density rapidly multiplies until the voltage supply is shorted (discharged). Ion interactions at the negative electrode introduce a mechanism to maintain a self-sustained discharge. Although the positive ions do not gain enough energy to ionize gas molecules during their transit, they may generate electrons at the negative electrode through secondary emission (Fig. 2b). This process is parametrized by the secondary emission coeficient γ. The coefficient is high at high ion energy (> 100 keV). The large value of reflects the fact that ions have a short stopping range in solid matter and deposit their energy near the surface. Ions in a gas-filled gap have low average energy. The secondary-emission coefficient has a nonzero value for slow ions because there is available energy from recombination of the ion with an electron at the surface. The secondary emission coefficient for a zero-velocity ion is in the range γ ~ 0.02.
With ion interactions, the total electron current density leaving the negative electrode consists of the source term plus a contribution from secondary emission. We define the following current densities: jo is the source, jc is the net current density leaving the negative electrode, ji is the ion current density arriving at the negative electrode, and ja is the total electron flux arriving at the positive electrode. Each ionizing collision creates one electron and one ion. By conservation of charge, the ion current is given by Eq. 9.38. The equation states that ions and electrons leave, the gap at the same rate in the steady state. The portion of the electron current density from the negative electrode associated with secondary emission is given by Eq. 9.39. Equation 9.39 implies the result of Eq. 9.40. By the definition of the Townsend coefficient α, we can write the total electron current arriving at the anode as Eq. 9.41. Combining Eqs. 9.40 and 9.41 leads to the result of Eq. 9.42.
Comparing Eq. (9.42) with (9.37), the effects of ion feedback appear in the denominator. The current density amplification becomes infinite when the denominator equals zero. When the conditions are such that the denominator of Eq. (9.42) is zero, a small charge at the negative electrode can initiate a self-sustained discharge. The discharge current grows rapidly over a time scale on the order of the ion drift time, heating and ionizing the gas. The end result is a spark (a high-current-density plasma channel). Equation 9.43 gives the condition for spark formation.
Calculation of the absolute value of α as a function of the gap parameters involves complex atomic physics. Instead, we will develop a simple scaling relationship for α as a function of gas pressure and electric field. Such a relationship helps to organize experimental data and predict breakdown properties in parameter regimes where data is unavailable. The ionization coefficient is proportional to the number of collisions between an electron and gas atoms per centimeter traveled, or α ~ 1\λ. The ionization coefficient also depends on the average electron drift energy, Eλ. The ionization rate is proportional to the fraction of collisions in which an electron enters with kinetic energy greater than the ionization energy of the atom, I. The properties of particles traveling through a random distribution of collision centers is treated in texts on atomic physics. The familiar result is that the distance between collisions is a random variable that follows the Poisson distribution of Eq. 9.44. The energy of a colliding electron is, by definition, T = xeV0/d. The fraction of collisions in which an electron has T > I is given by the integral of Eq. 9.44 from x = Id/eV0 to infinity. The result of these considerations is that α is well described by the scaling law of Eq. 9.45. The quantities A and B are determined from experiments or detailed collision theory. Equation 9.45a, the gap voltage for sparking, follows from substitution of Eq. 9.45 into 9.43. Solving for the sparking voltage Vs gives the main result, Eq. 9.46.
Equation 9.46 is known as Paschen's law [F.Paschen, Wied. Ann. 37, 69 (1889)] for gas breakdown. The sparking voltage is a function of the product pd and constants that depend on the gas properties. The values of A and B are relatively constant over a wide voltage range when the average electron energy is less than I. Furthermore, Vs is insensitive to γ; therefore, the results are almost independent of the electrode material. Figure 3 shows a normalized plot of Vs versus pd. The sparking voltage reaches a minimum value Vs,min at a value pdmin. Voltage hold-off increases at both low and high values of pd. Voltage hold-off is high at low pd because there is a small probability that an electron will strike a molecule while traveling between electrodes. At high values of pd, Vs ~ pd . In this regime, electrons undergo many collisions, but the mean free path is short. Few electrons gain enough energy to produce an ionization.
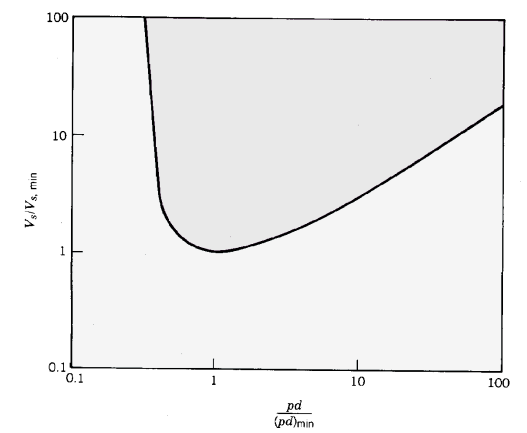
Figure 3. Normalized Paschen curve: sparking voltage versus the product of pressure and gap width.
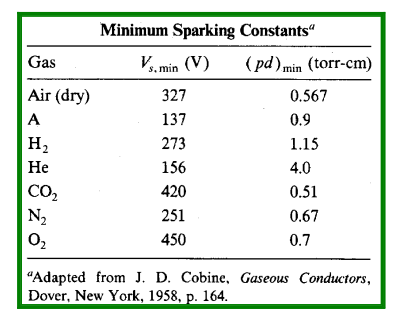
Equation 9.46 can be rewritten as Eq. 9.47. The table below shows the spark parameters for some common gases. The minimum sparking voltage is high for electronegative gases like oxygen and low for gases with little probability of electron capture like helium and argon. In electronegative gases, there is a high probability that electrons are captured to form negative ions. The heavy negative ions cannot produce further ionization, so that the electron is removed from the current multiplication process.
LINKS